高等数学解题常用公式笔记总结

发布时间：2023-12-24 06:18:57

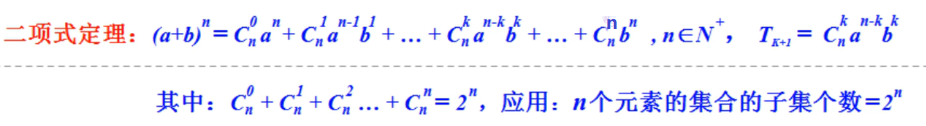
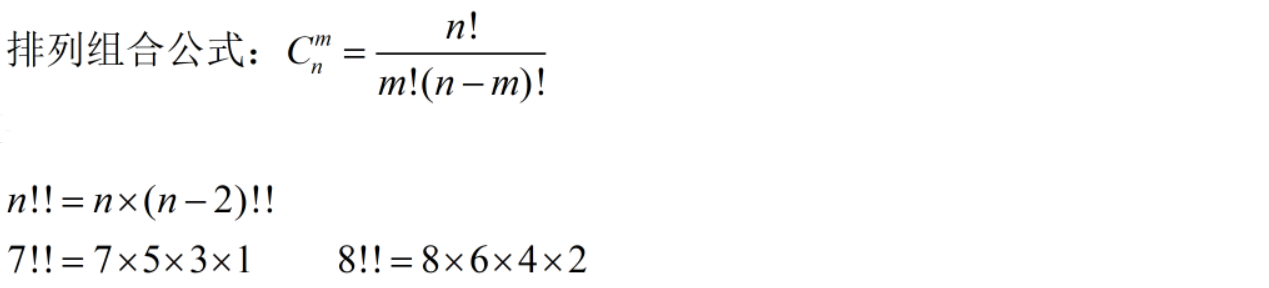
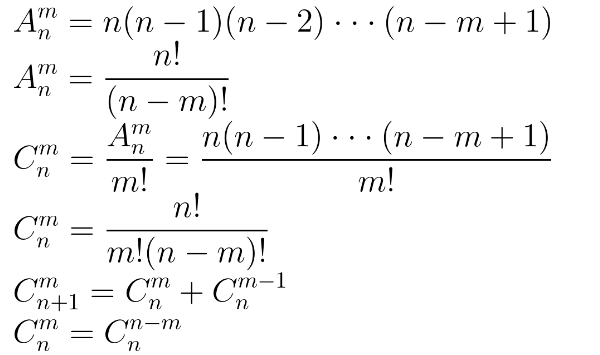
在这里插入图片描述

————————————————————————————————————————————————————————————
在这里插入图片描述
————————————————————————————————————————————————————————————
在这里插入图片描述
————————————————————————————————————————————————————————————

在这里插入图片描述

————————————————————————————————————————————————————————————

在这里插入图片描述

文章目录

一、等价无穷小

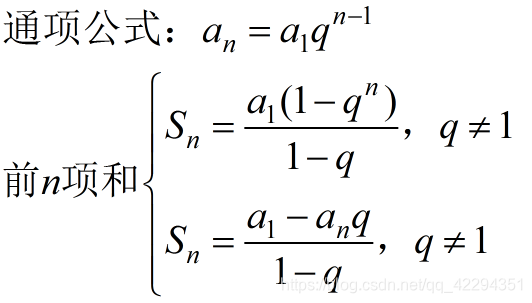
在这里插入图片描述

二、等差数列

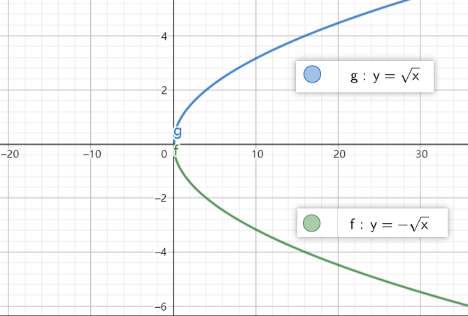
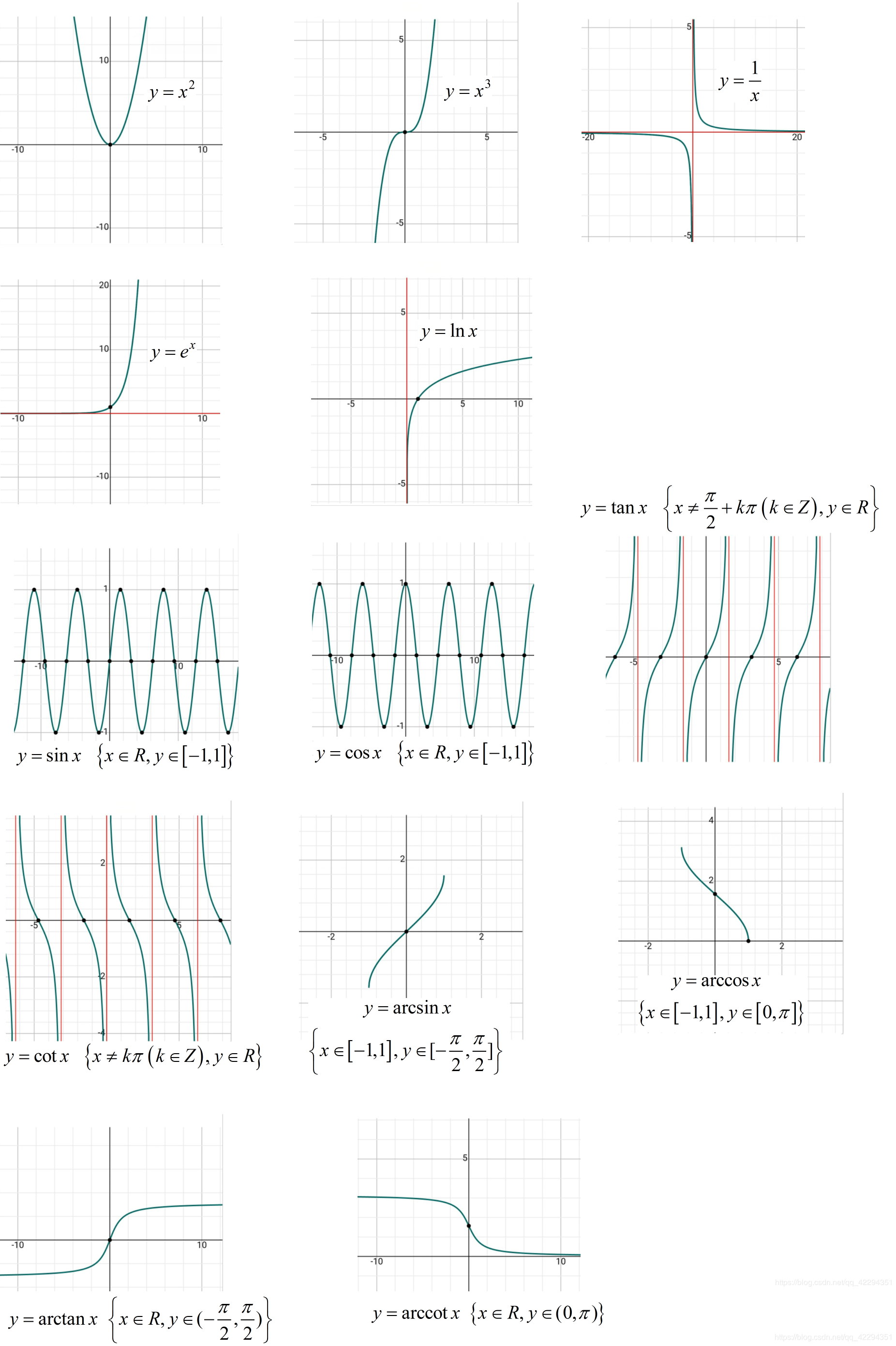
在这里插入图片描述

三、等比数列

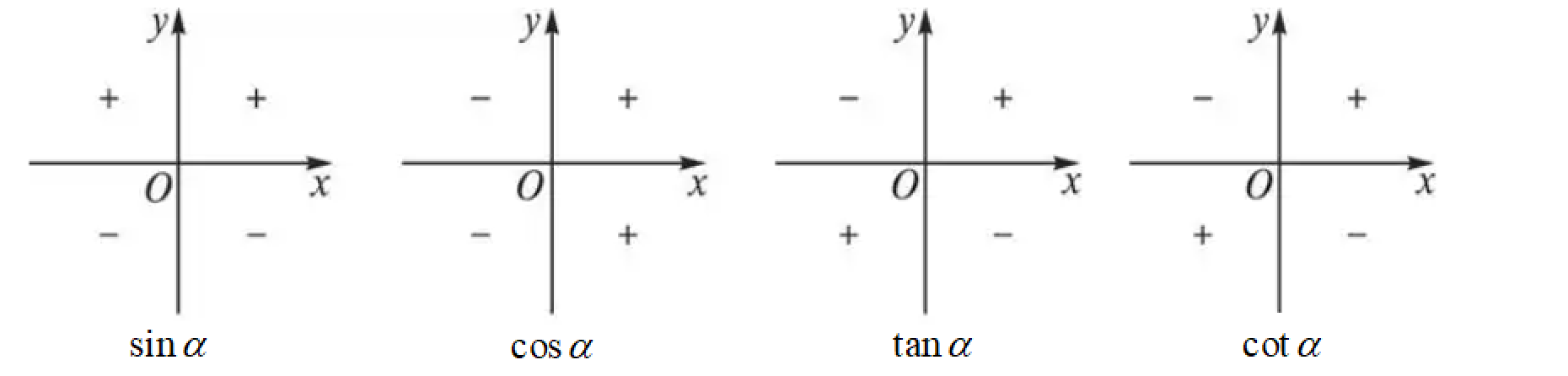
在这里插入图片描述

四、不定积分

在这里插入图片描述

代换

在这里插入图片描述

五、基本函数图像

在这里插入图片描述

在这里插入图片描述

六、三角函数

在这里插入图片描述

一全正二正弦三正切四余弦

在这里插入图片描述

反三角函数公式（常用）

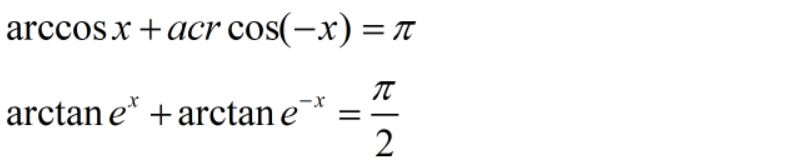
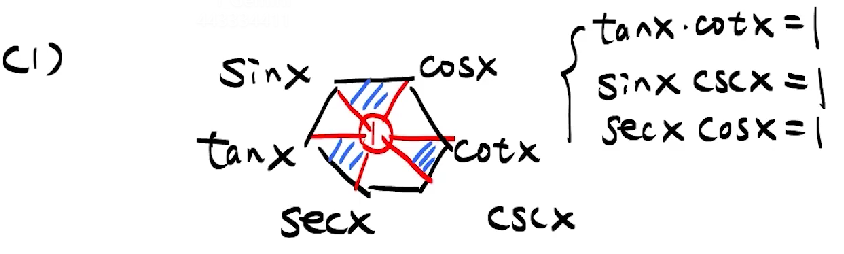
在这里插入图片描述

在这里插入图片描述

三角函数之间的关系

对角相乘为1
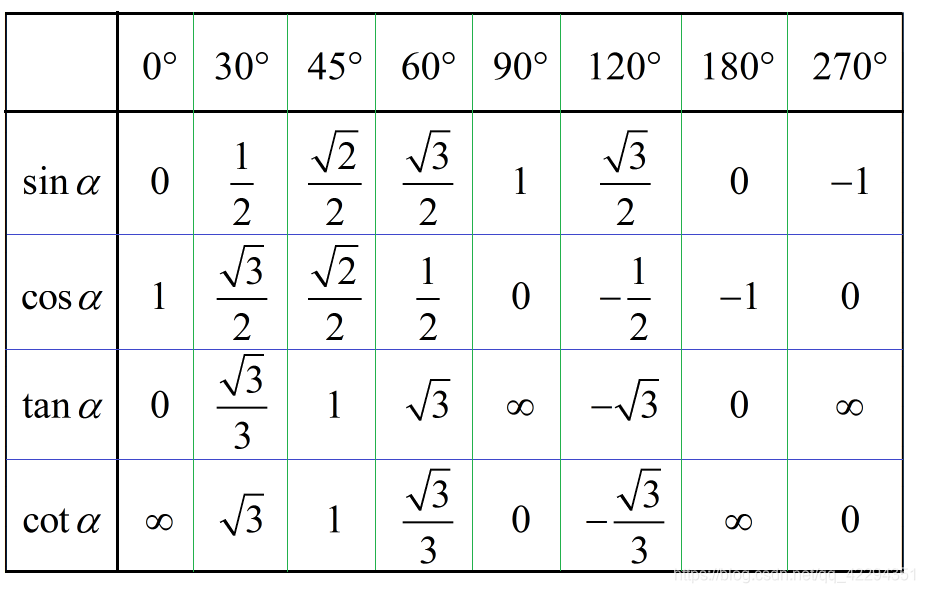
在这里插入图片描述

特殊角

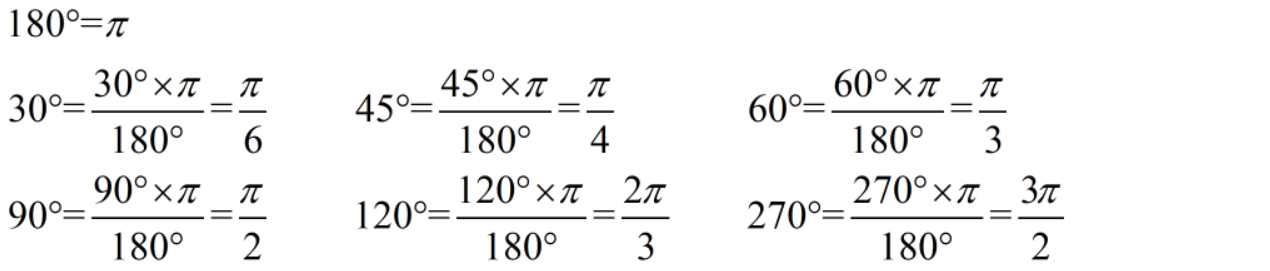
在这里插入图片描述

角度与π的转换

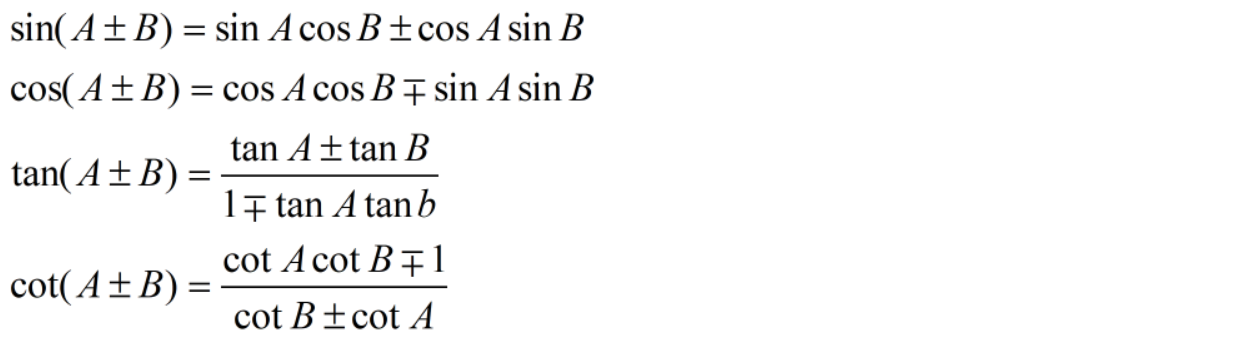
在这里插入图片描述

两角和公式

在这里插入图片描述

倍角公式

在这里插入图片描述

三倍角公式（不重要）

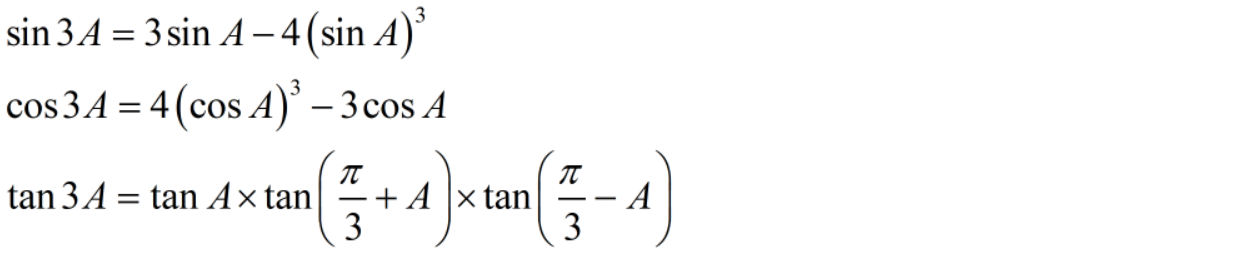
在这里插入图片描述

半角公式

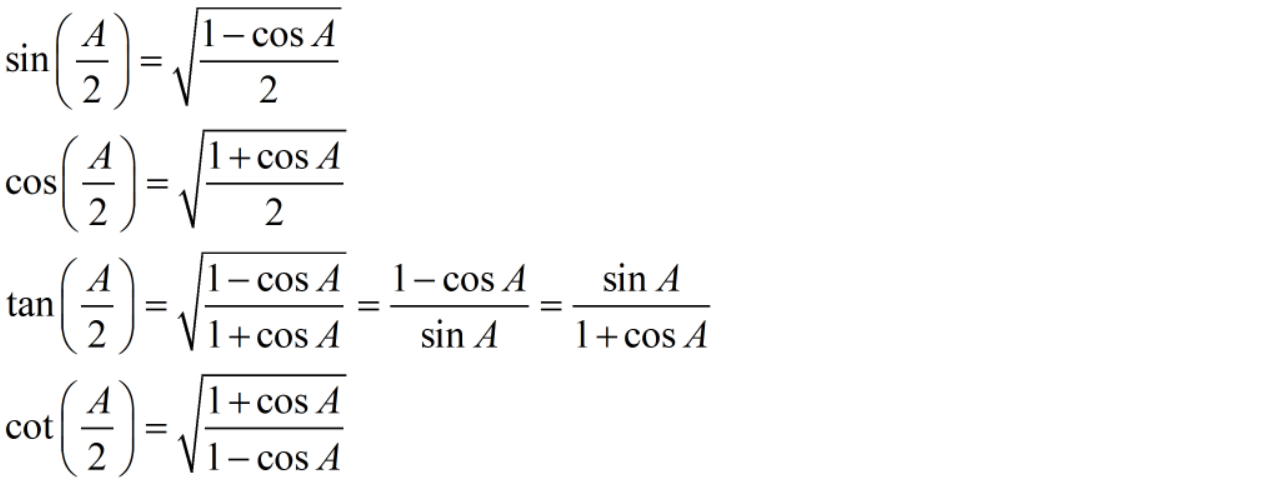
在这里插入图片描述

万能公式

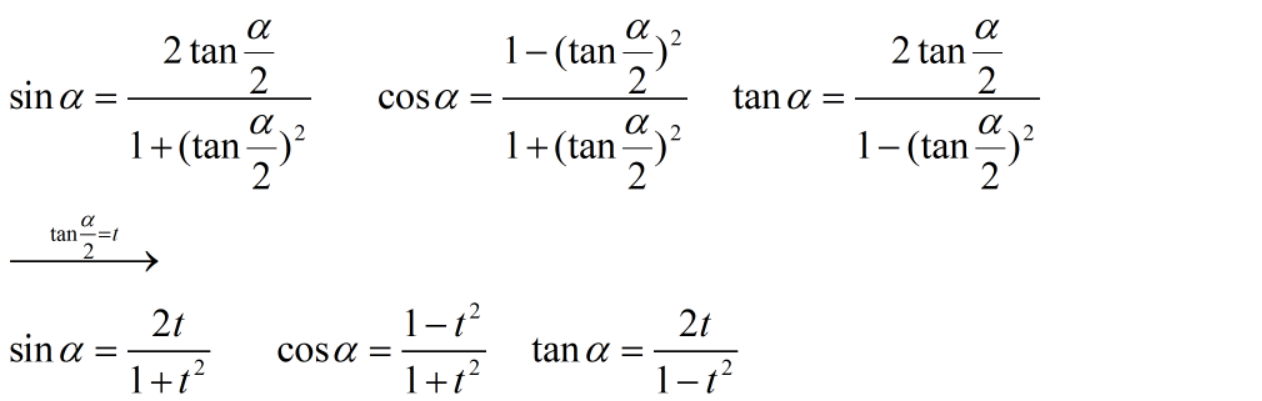
在这里插入图片描述

和差化积

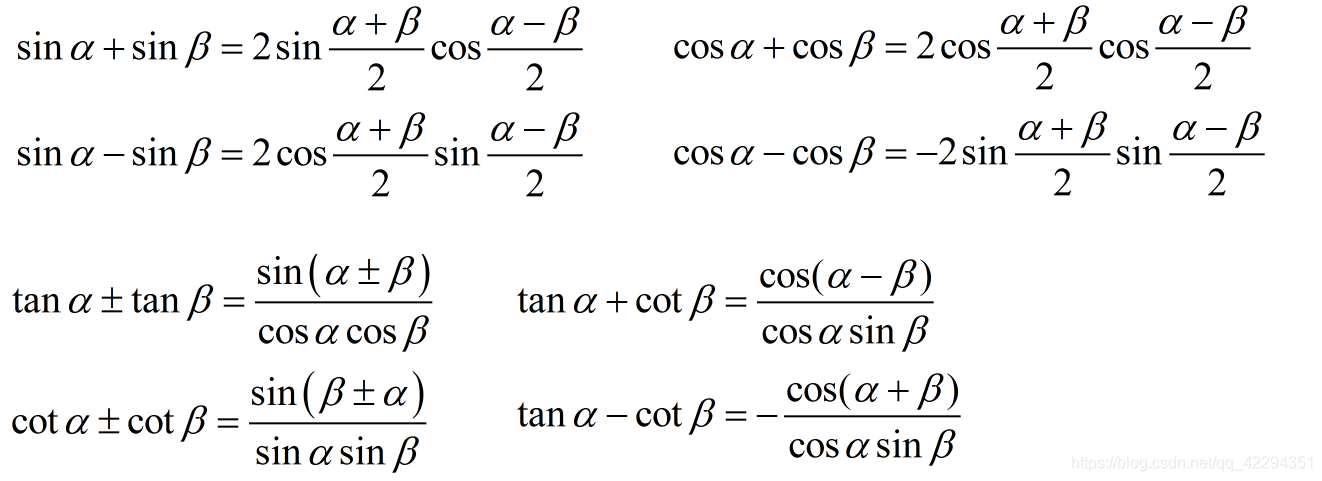
在这里插入图片描述

七、定积分

需要记忆的一些定积分结果

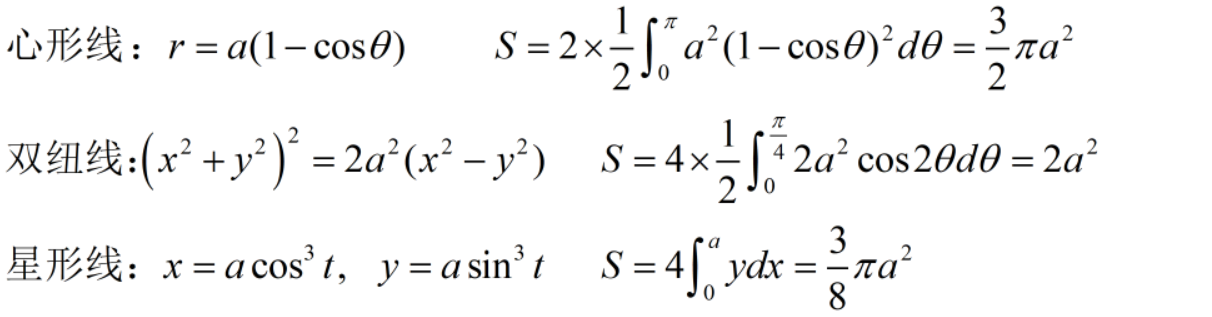
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

定积分常用公式

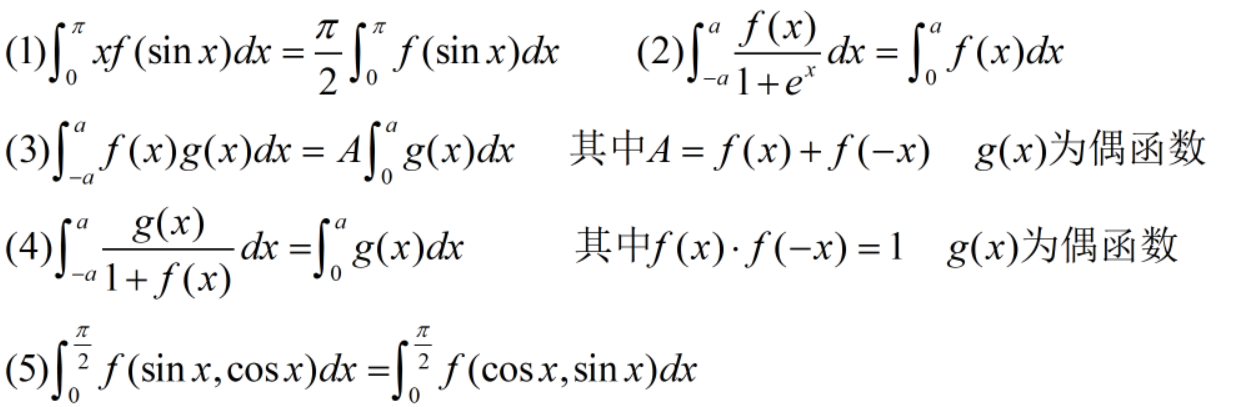
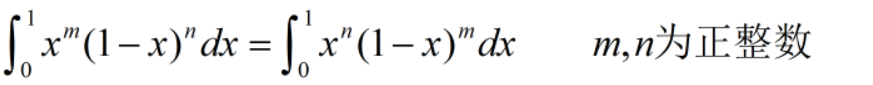
在这里插入图片描述
在这里插入图片描述

偶倍奇零

第一个是被积函数 f ( x ) f(x) f(x)为非奇非偶时候可以用
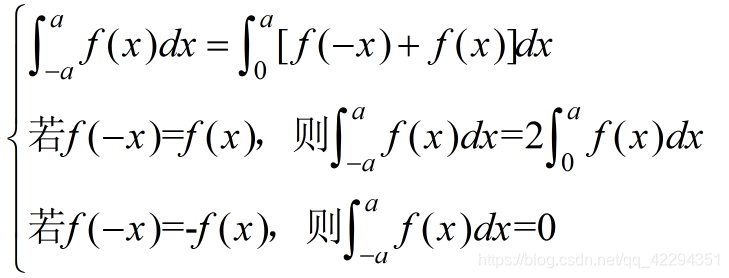
在这里插入图片描述

区间再现

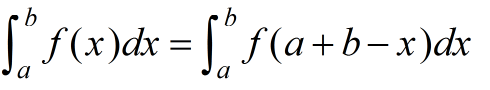
在这里插入图片描述

华里士公式(点火公式)

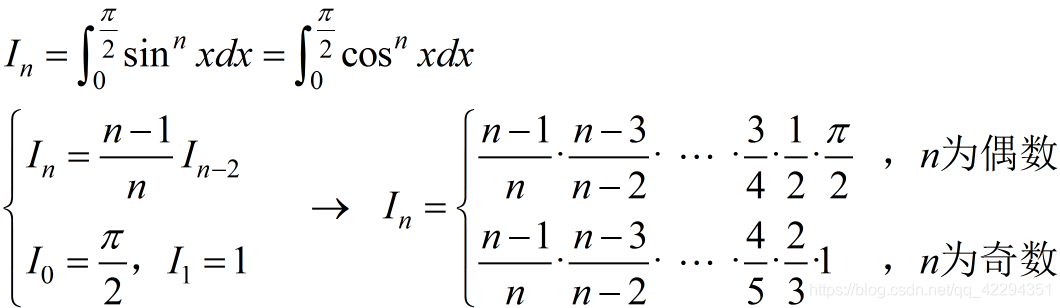
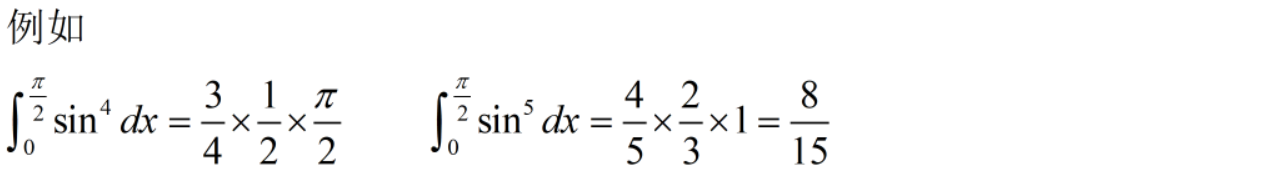
在这里插入图片描述
在这里插入图片描述

周期函数

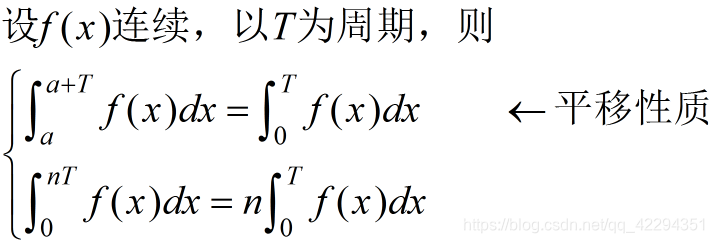
在这里插入图片描述

诱导公式

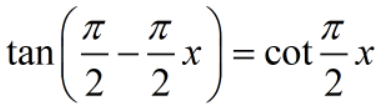
在这里插入图片描述
在这里插入图片描述

反常积分(广义积分)

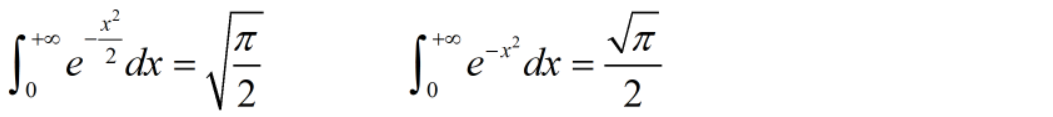
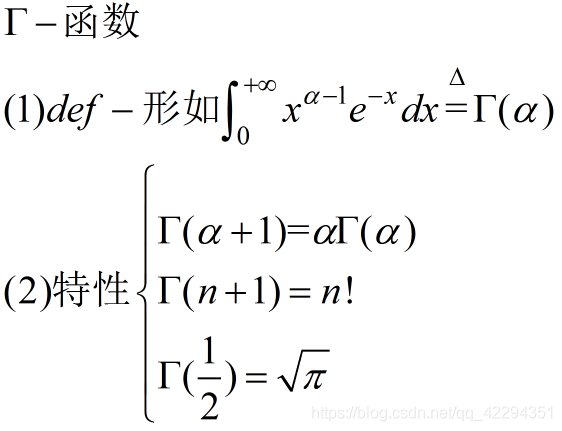
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

补充

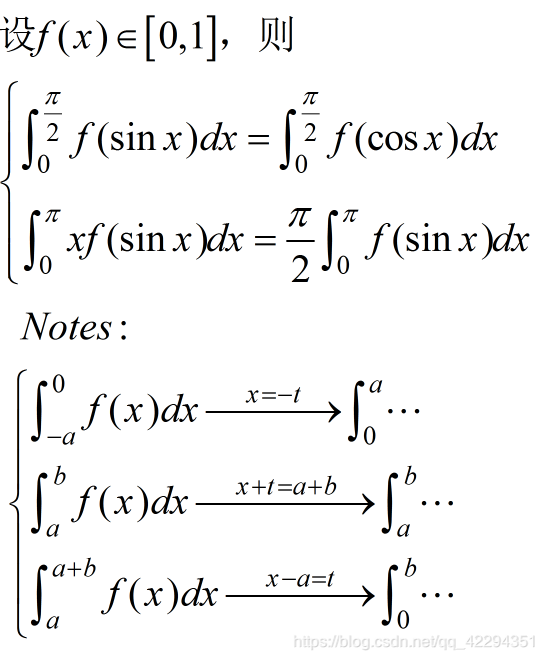
在这里插入图片描述

变限积分

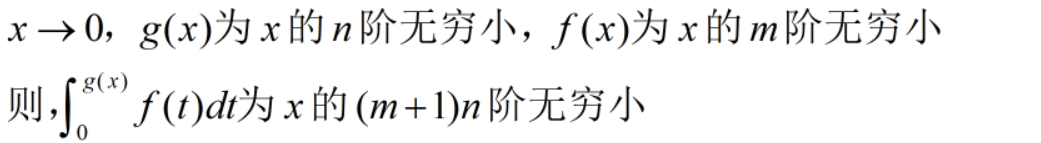
在这里插入图片描述

八、微分方程

一阶线性微分方程

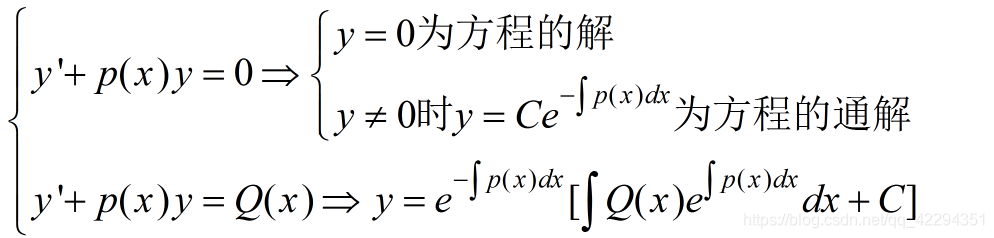
在这里插入图片描述

二阶常数项齐次线性微分方程

在这里插入图片描述

n阶常数项齐次线性微分方程

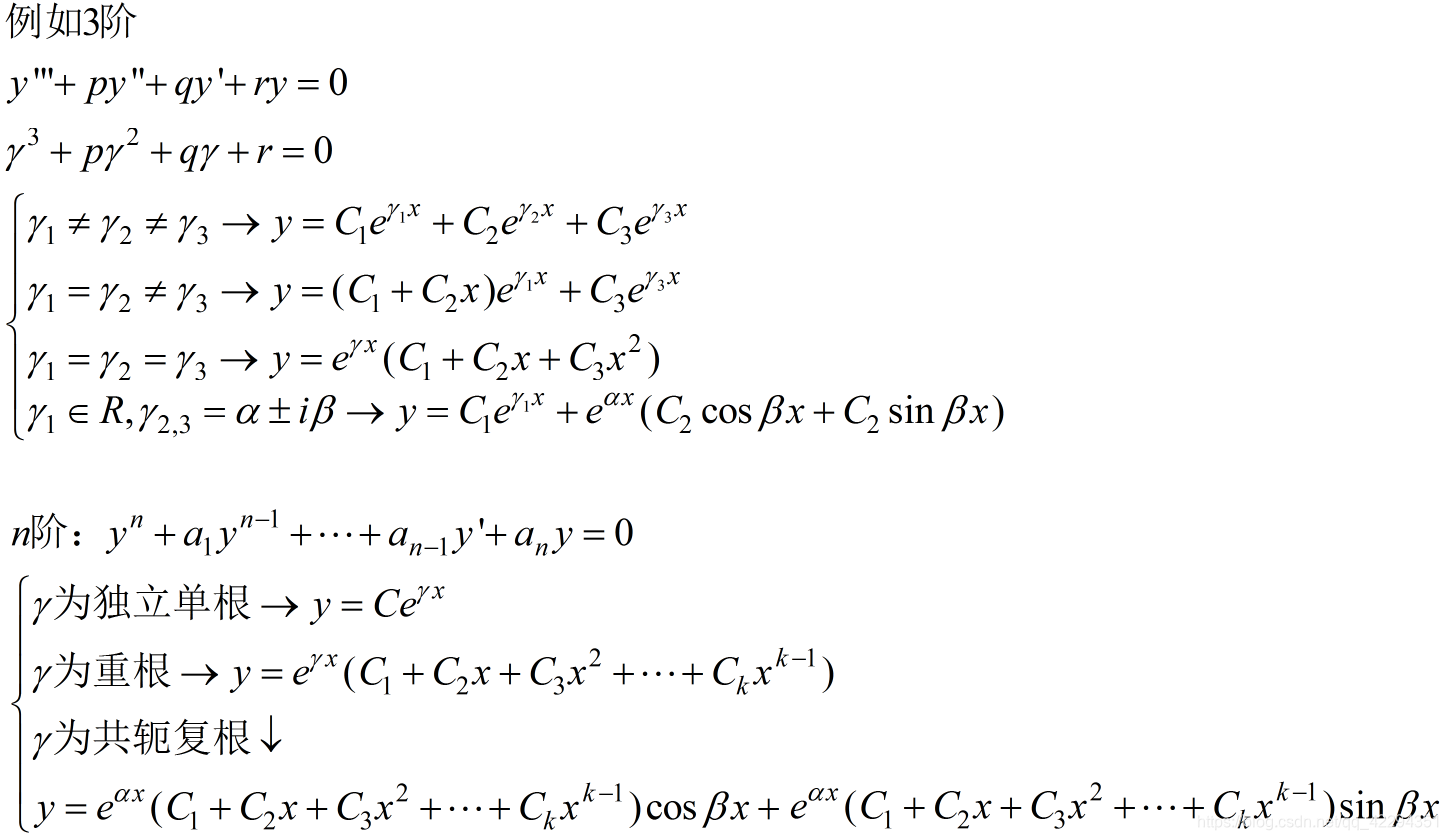
在这里插入图片描述

二阶常数项非齐次线性微分方程

在这里插入图片描述

一阶全微分方程

在这里插入图片描述

九、泰勒公式

在这里插入图片描述

常见麦克劳林展开式

其实用的最多的是这些展开式，级数求和函数中经常用前5个
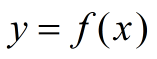
在这里插入图片描述

十、渐近线

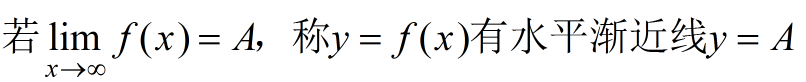
在这里插入图片描述

水平渐近线

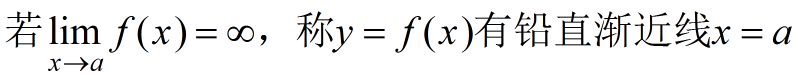
在这里插入图片描述

铅直渐近线

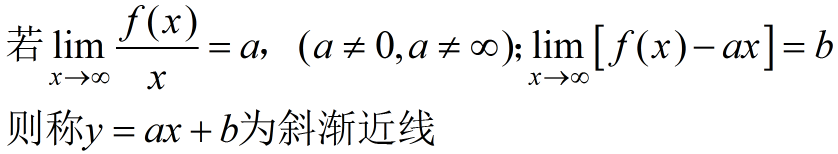
在这里插入图片描述

斜渐近线

在这里插入图片描述

十一、向量代数与空间解析几何

向量的模

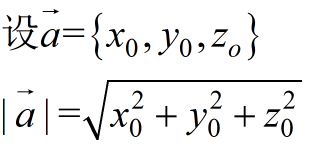
在这里插入图片描述

方向角与方向余弦

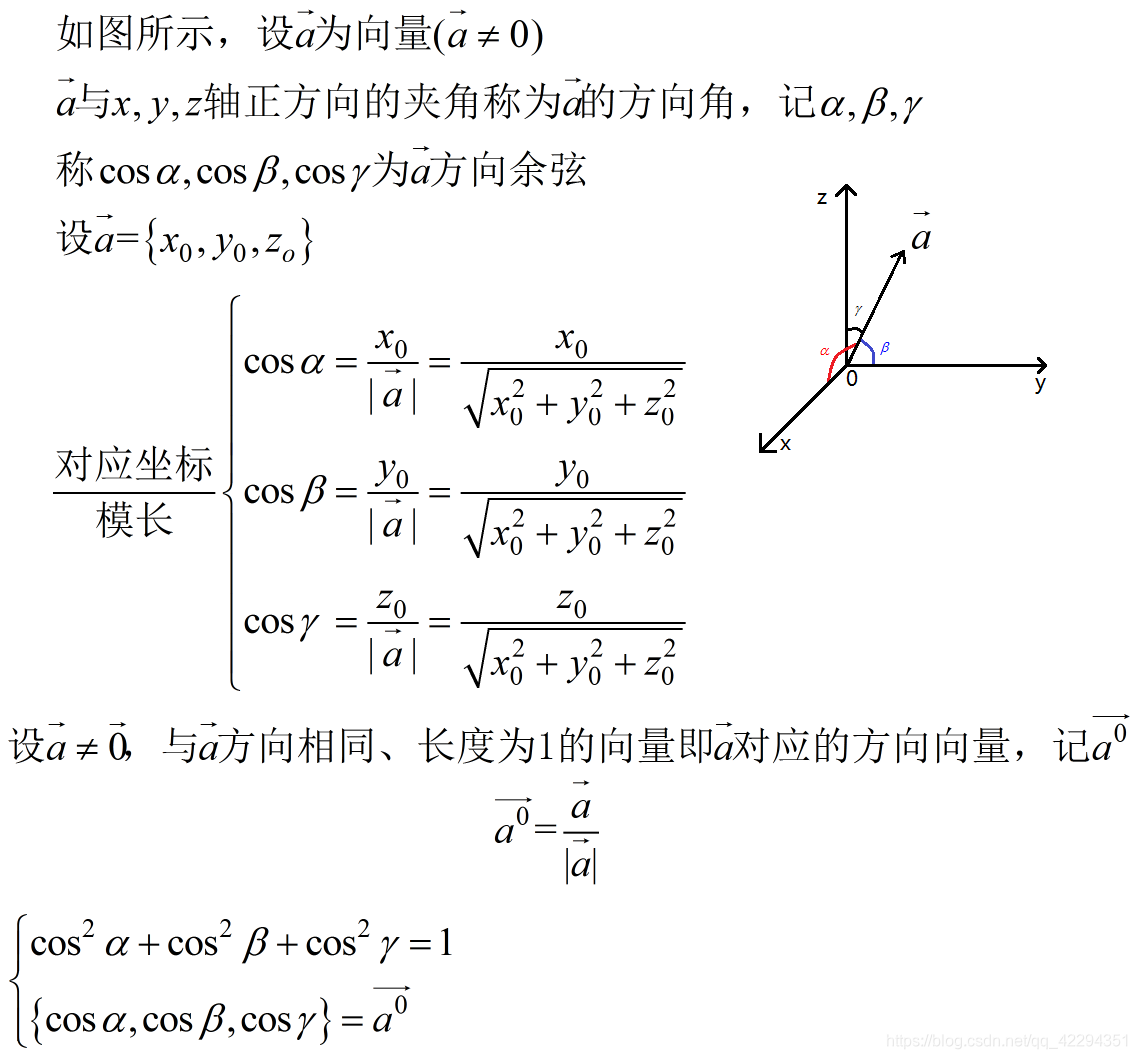
在这里插入图片描述

单位向量

模长为1的向量

单位化

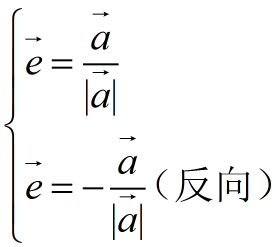
在这里插入图片描述

投影

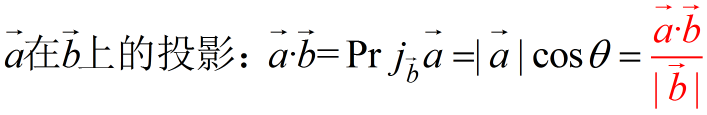
在这里插入图片描述

数量积（点乘）

参与运算的是向量，结果为数
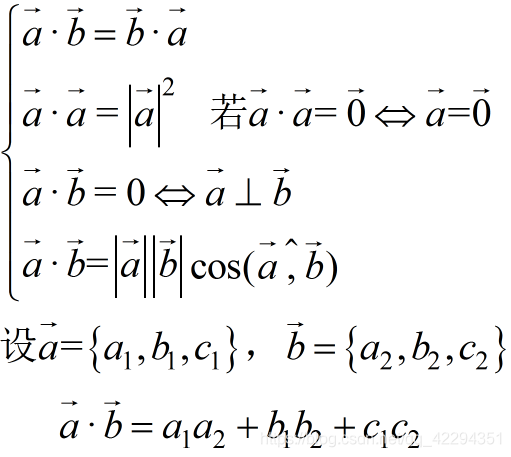
在这里插入图片描述

向量积（叉乘）

参与运算的是向量，结果还是向量
在这里插入图片描述

十二、方向导数与梯度

方向导数(是个数)

cos为方向余弦
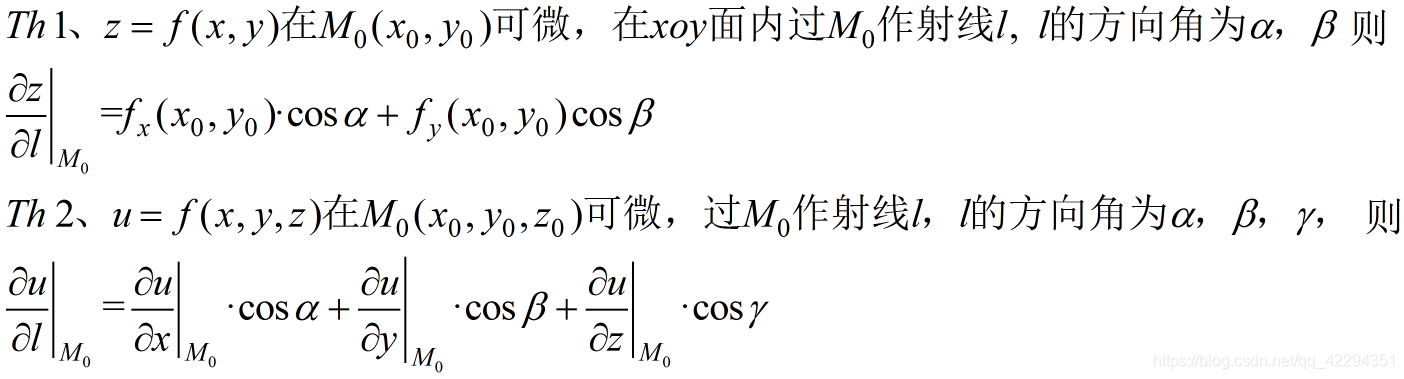
在这里插入图片描述

梯度

在这里插入图片描述
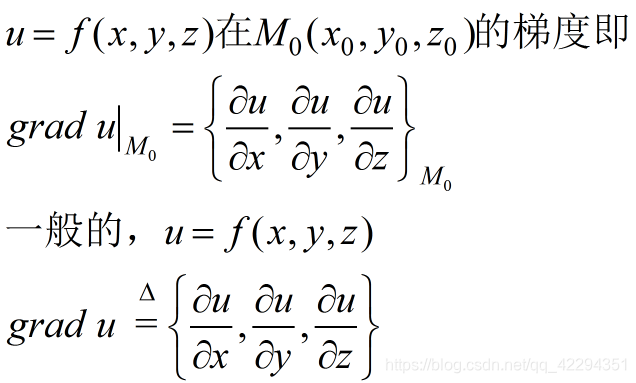
梯度方向即函数增长速度最快的方向或方向导数取最大值的方向

方向导数与梯度的关系(梯度的模)

在这里插入图片描述

十三、标准几何体表面积/体积公式

首先声明：
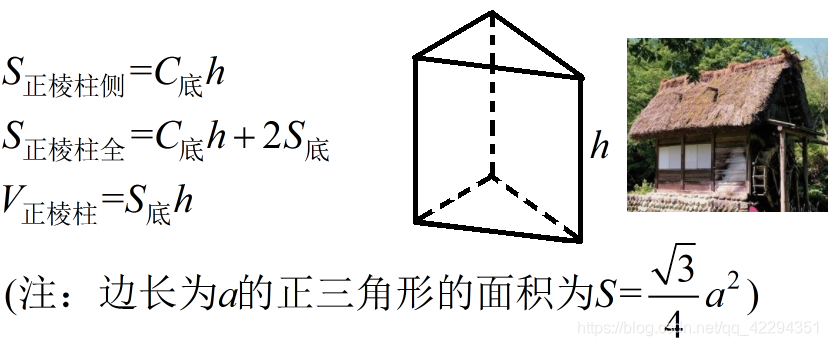
在这里插入图片描述

棱柱与棱锥

棱柱

在这里插入图片描述

棱锥

在这里插入图片描述

圆柱、圆锥、球

圆柱

在这里插入图片描述

圆锥

在这里插入图片描述

球

在这里插入图片描述

十四、定理

介值定理

英文表述就是：The value between m and M.
观察一下，只有这俩个定理属于闭区间
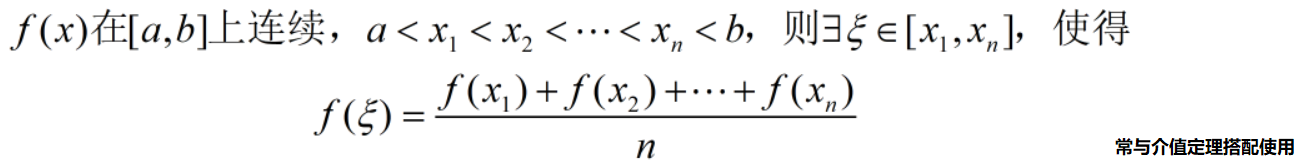
在这里插入图片描述

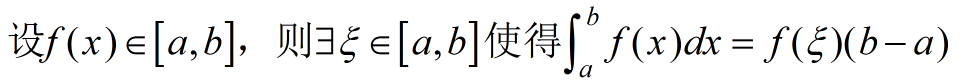
在这里插入图片描述

函数平均值定理

在这里插入图片描述

积分中值定理

在这里插入图片描述

升级版积分中值定理（用拉格朗日）

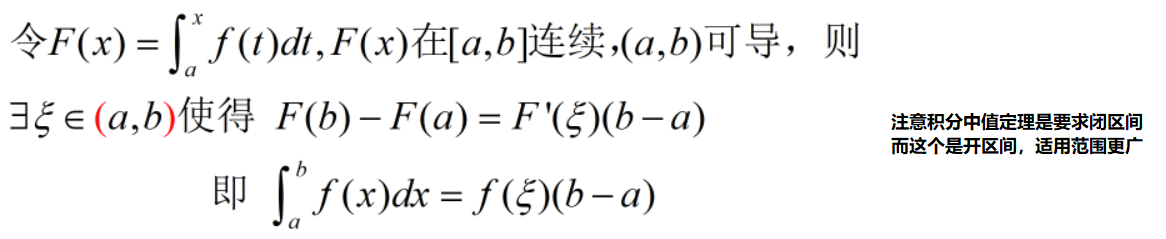
在这里插入图片描述

零点定理

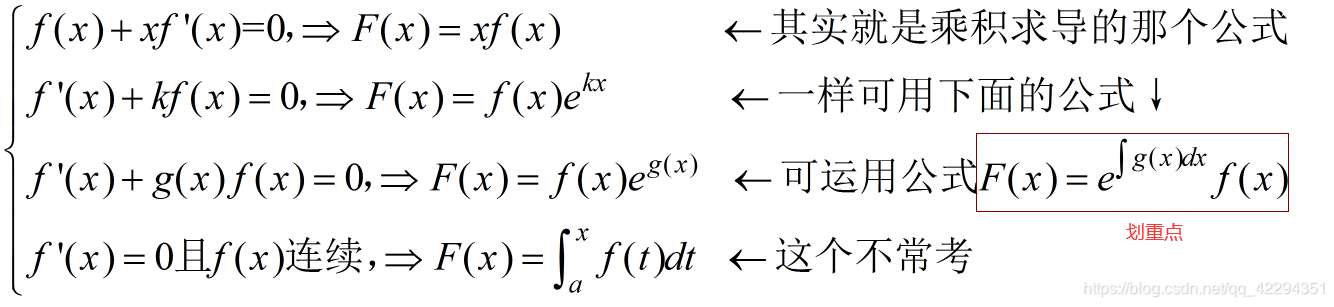
在这里插入图片描述

罗尔中值定理

在这里插入图片描述
在这里插入图片描述

拉格朗日中值定理

在这里插入图片描述
在这里插入图片描述

柯西中值定理

在这里插入图片描述

二重积分中值定理

在这里插入图片描述

积分第一中值定理

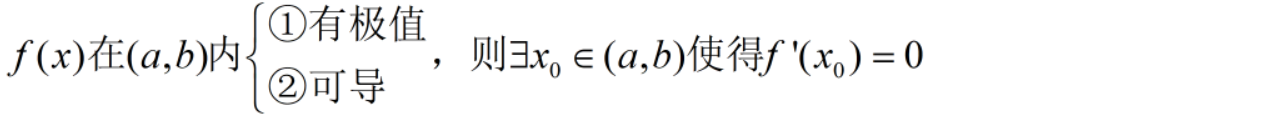
在这里插入图片描述

费马定理

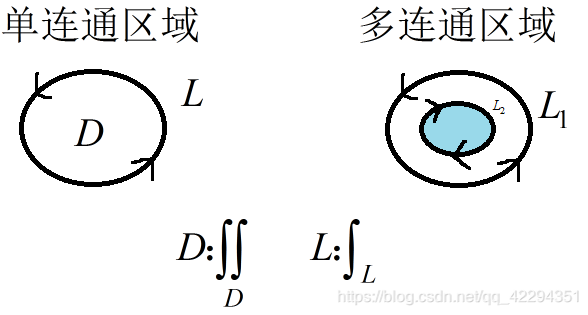
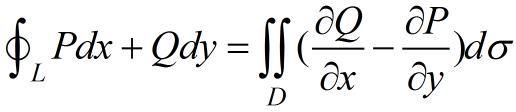
在这里插入图片描述

十五、格林公式

在这里插入图片描述
在这里插入图片描述
正向：逆时针
逆向：顺时针（钟表方向）[需要加负号]
因为内容比较少也不算太难，直接加这里了。
在这里插入图片描述
在这里插入图片描述

十六、无条件极值

在这里插入图片描述
在这里插入图片描述

十七、旋转体体积公式

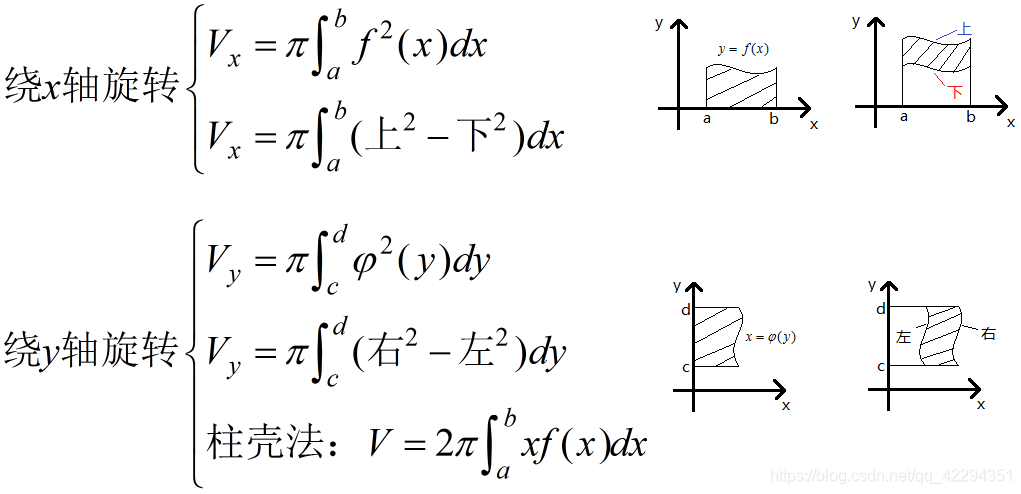在这里插入图片描述旋转体体积公式其实是可以由元素法推出来的，详情：元素法的应用

十八、定义求导

在这里插入图片描述

十九 三重积分

在这里插入图片描述

二十 高斯公式

在这里插入图片描述

二十一 曲率与曲线半径

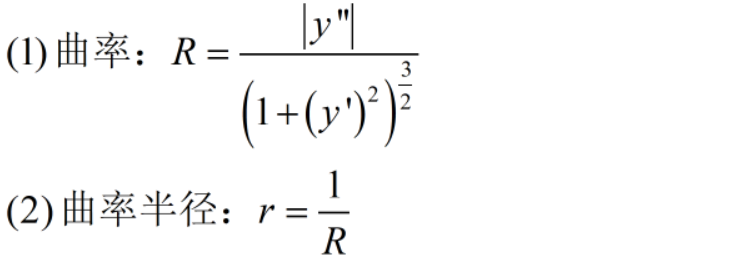
在这里插入图片描述

常用导数恒等式

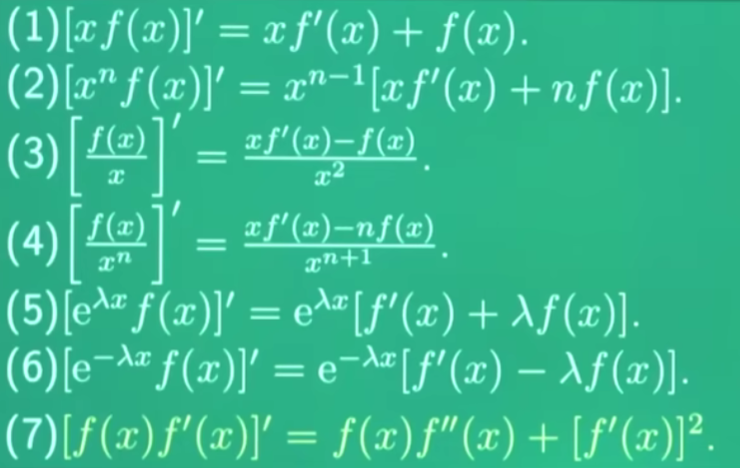
在这里插入图片描述

补充

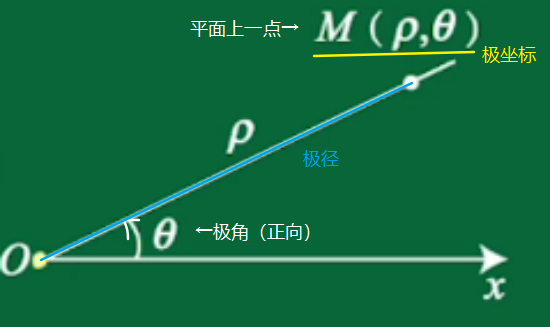
1 极坐标

在这里插入图片描述
在这里插入图片描述

2 一元二次方程

a x 2 + b x + c = 0 ax^2+bx+c=0 ax2+bx+c=0
△ = b 2 ? 4 a c △=b^2-4ac △=b2?4ac
△ > 0 x 1 , 2 = ? b ± b 2 ? 4 a c 2 a △>0\quad x_{1,2}=\frac{-b±\sqrt{b^2-4ac}}{2a} △>0x1,2?=2a?b±b2?4ac ??
△ = 0 x 1 = x 2 △=0\quad x_1=x_2 △=0x1?=x2?重根
△ < 0 △<0\quad △<0两个负根 ?例如： i 2 = ? 1 ? 9 = ± 3 i i^2=-1\quad \sqrt{-9}=±3i i2=?1?9 ?=±3i
根与系数关系： x 1 + x 2 = ? b a ， x 1 × x 2 = c a x_1+x_2=-\frac{b}{a}，x_1×x_2=\frac{c}{a} x1?+x2?=?ab?，x1?×x2?=ac?

例： 求解 4 y ′ ′ + 4 y ′ + 5 y = 0 4y''+4y'+5y=0 4y′′+4y′+5y=0
解：
4 λ 2 + 4 λ + 5 = 0 4λ^2+4λ+5=0 4λ2+4λ+5=0
△ = b 2 ? 4 a c = 16 ? 4 × 5 = 16 ? 80 < 0 △=b^2-4ac=16-4×5=16-80<0 △=b2?4ac=16?4×5=16?80<0
λ 1 , 2 = ? 4 ± ? 64 2 × 4 = ? 4 ± i 8 8 = ? 1 2 ± i = α ± β i λ_{1,2}=\frac{-4±\sqrt{-64}}{2×4}=\frac{-4±i8}{8}=-\frac{1}{2}±i=α±βi λ1,2?=2×4?4±?64 ??=8?4±i8?=?21?±i=α±βi
即 α = ? 1 2 ， β = 1 α=-\frac{1}{2}，β=1 α=?21?，β=1
综上，通解为 y = e α x ( C 1 c o s β x + C 2 s i n β x ) y=e^{αx}(C_1cosβx+C_2sinβx) y=eαx(C1?cosβx+C2?sinβx)
??????? = e ? 1 2 x ( C 1 c o s x + C 2 s i n x ) =e^{-\frac{1}{2}x}(C_1cosx+C_2sinx) =e?21?x(C1?cosx+C2?sinx)

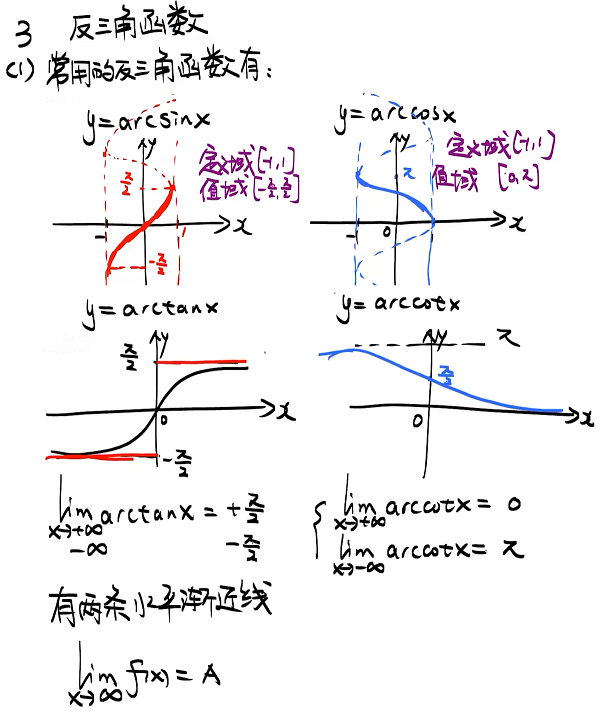
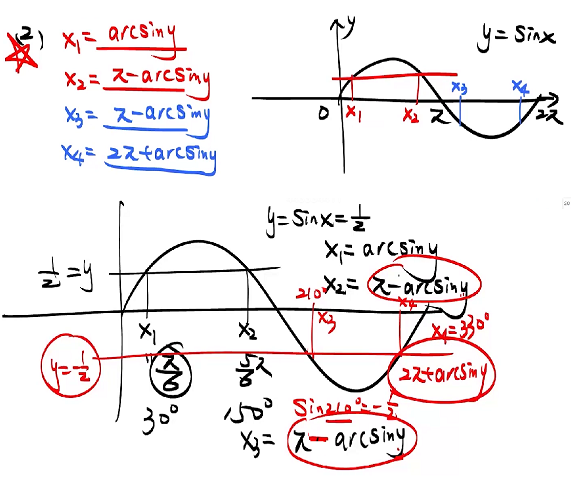
3 反三角函数

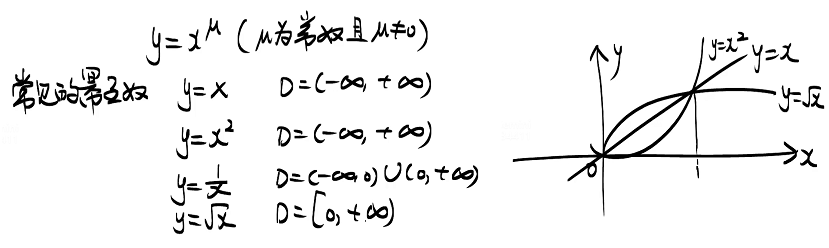
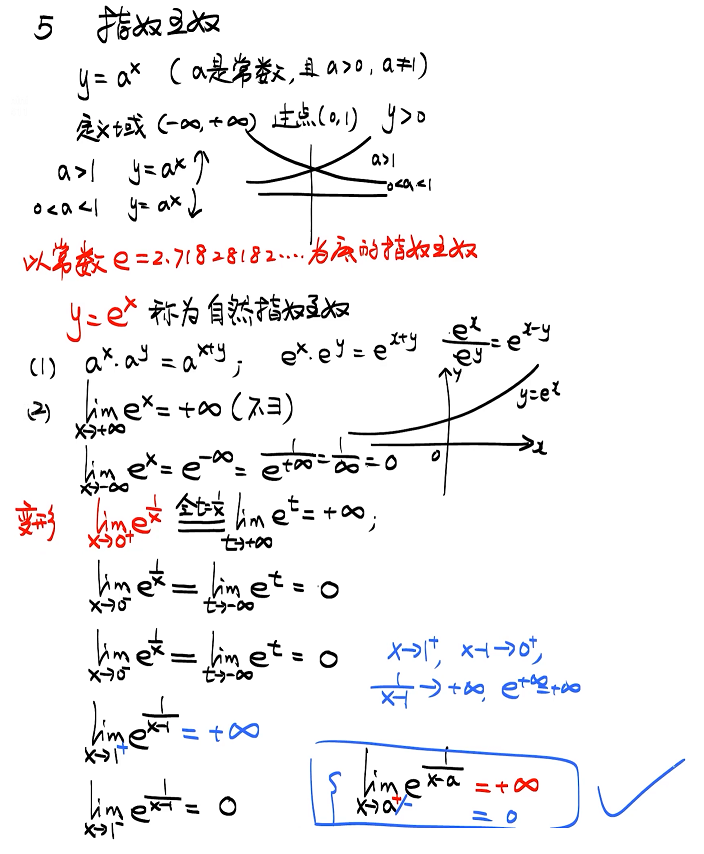
在这里插入图片描述

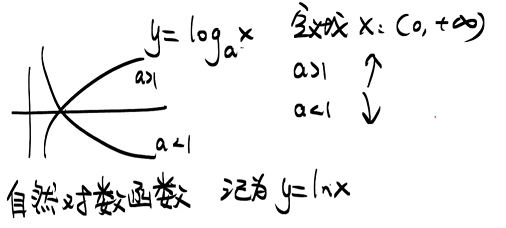
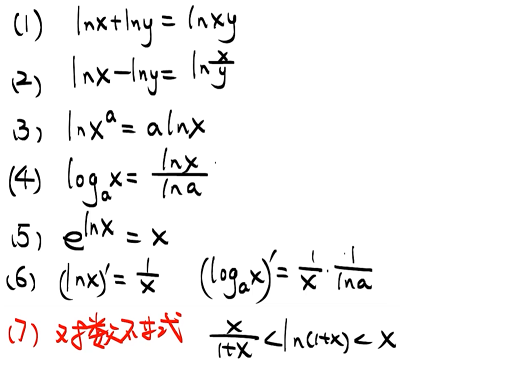
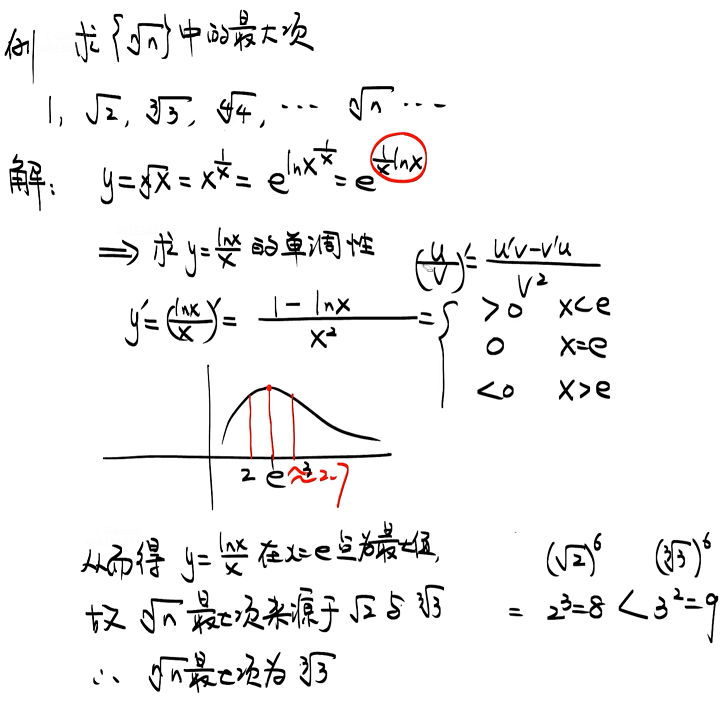
在这里插入图片描述

4 幂函数

在这里插入图片描述

5 指数函数

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

6 对数函数

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

7 乘法与因式分解

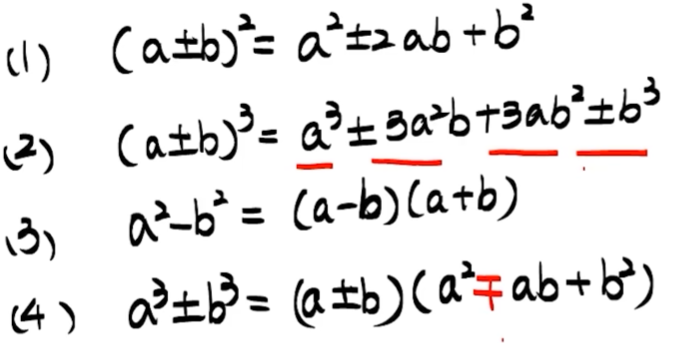
在这里插入图片描述
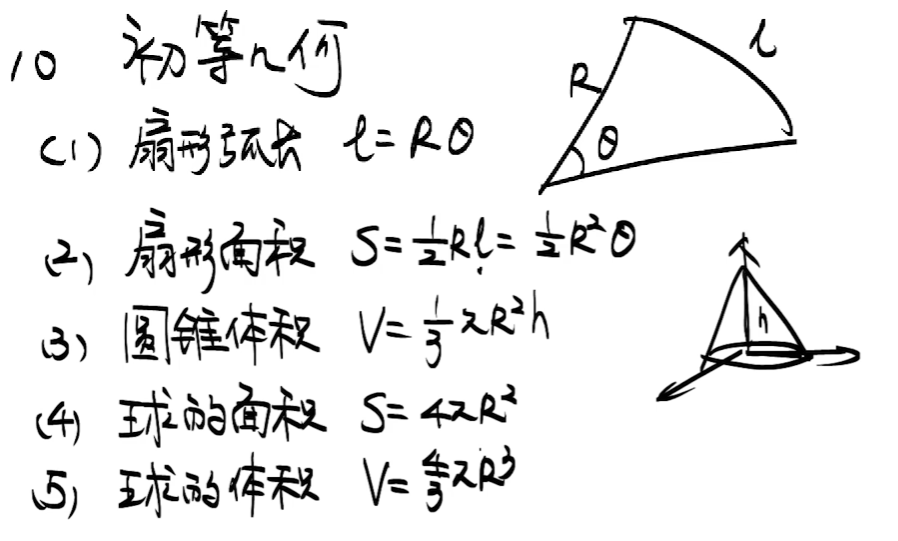
在这里插入图片描述

在这里插入图片描述

8 数列求和

在这里插入图片描述
在这里插入图片描述

9 解析几何

在这里插入图片描述

10 初等几何

在这里插入图片描述

11 不等式

在这里插入图片描述

文章来源:https://bigxie.blog.csdn.net/article/details/106582906
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章