理解OSRM(4)-MLD算法总览

转载自这里。

Multi-Level Dijkstra算法来源自CRP算法论文Customizable route planning in road networks.。

设计目标

• 应用于大陆级别的实际路网数据
• 支持任意类型metric(可以理解为cost function)
• 响应时间满足实时查询的需求
• 快速的路况更新以及定制化metric更新

---

主要思想

实际路网由拓扑结构和metric属性两部分组成。路网拓扑结构由道路的一系列静态属性组成，包括道路长度，转向类型，车道数，道路类型，最大速度等；metric属性代表经过一条道路或转向时的实际cost。我们认为路网拓扑将结构是各个metric通用的并且很少变化，metric 属性可能会经常变化并且可以是用户定制的。
crp 算法包括以下三个阶段:

• metric-independent processing:处理路网拓扑数据，运行较慢，但是运行频率低
• metric customization:处理每个metric的时候都必须运行，要求执行速度快
• query stage:响应时间需满足实时查询

需要注意的是，针对一个指定的metric，crp算法的响应时间不如像ch等具有很好等级特性的算法，crp 算法的优势是在满足实时查询的基础上可以快速应用各种不同metric。

---

主流路径规划算法

• 以ch为代表的strong hierarchy 算法，依赖于道路等级特性进行数据预处理，响应时间快，对于等级特性差的metric加速效果变差(最短距离比最短时间慢10倍)，缺点是不能很好的支持各种metric
• 以A*,ALT为代表目标启发式算法，算法特点是相比ch,可以更好的支持多种metric，算法缺点是响应时间较慢。
• 基于图分割的路径规划算法，把路网处理为多层overlay graph,算法的特点是图分割和响应时间和metric相互独立，适用于crp算法的设计思路。（图的覆盖可以参见维基百科）

---

分割图

分割图的一些说明

• 一个node 属于且仅属于同一层的唯一一个cell;
• 每一层cell 中的node数小于设定的参数U(每层不一样);
• 对于一个cell 来说其对应的高层的cell记为supercell,其对应的低层的cell记为subcell;
• 处于cell边界的所有node记为boundary vertex,相同level连接不同cell的边记为boundary arc;
• 对于cell中每两个boundary vertex在当前cell内计算最短路径，这些最短路径记为shortcut或clique;
• 可以证明，level-l中的所有boundary arc以及所有clique是level-(l-1)的覆盖图;
• Holzer et al在文献中证明覆盖图可以保证搜索的正确性。

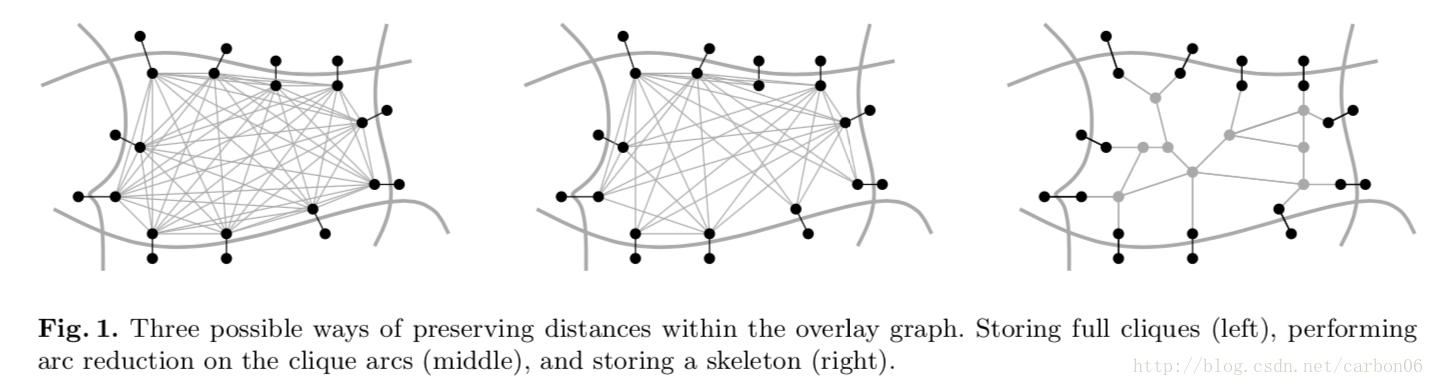
对分割图剪枝

• reduction: 针对每两个boundary vertex在本层graph 上进行dijkstra搜索，把之前计算的不是shortcut 的边删除；
• skeleton graph:针对每个boundary vertex计算到当前cell内其他boundary vertex的最短路径树，最后对所有的最短路径树求并集构造为 skeleton graph。

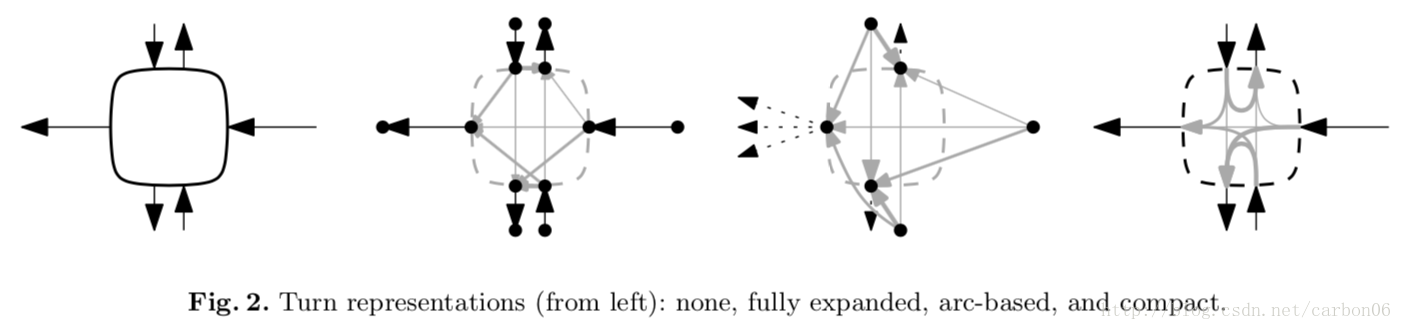
针对转向的建模

• fully expanded:对交叉路口的每个入口出口添加node,可能的转向方向添加edge；
• arc-based:只添加每个可能方向出口的节点；
• compact:构建一个p*q的turn table(p 代表的交叉路口的入口，q 代表交叉路口的出口),由于交叉路口的类型有限，所有对于每个交叉路口节点存储一个指向turn table的指针。

---

基于多层overlay graph 的路径规划

Partition

crp 提出基于多层overlay graph 的路径规划算法性能依赖于每层中boundary arc的数目。

Partition 阶段的目标是使得 oveylay graph 中boundary arc的数目尽量少。这里crp 算法使用的partition算法是PUNCH，参见PUNCH。PUNCH算法的原理是利用路网中自然分割(河流，山川，高速公路)作为启发因子进行分割。
PUNCH算法相比其他图分割算法性能有两倍提升，但是算法运行时间相比其他算法运行时间较长，这点无伤大雅，因为partition过程的过程属于离线流程，不会经常运行。

Overlay 拓扑

我们在partition的过程中进行的是nested partition,因此对于在overlay graph 中任意一个node都存在于低level的overlay graph 中，因此我们只需要存储一份node的集合，每个node都有一个标记来标记对于某个level来说，其是不是一个bourdary vertex。

对于每一个cell来说，其有p个入口节点，q个出口节点，我们使用一个p*q的矩阵W来存储所有shortcut,也就是计算前面提到的clique。需要注意的是，W的内容在partition阶段不进行计算，具体数值在customization阶段结算;且每一个metric 对应着一个W。

Customization

Customization 阶段会在query的同时进行，因此Customization阶段需要足够快，Customization的过程实际上就是计算上面提到的W。

我们采用自底向上的方式针对每个cell计算W。

加速Customization计算

Impoving Locality

在计算level i 的Cell C 的时候，我们需要的计算过程是在整个相应的overlay graph 中限制在Cell C的范围内搜索，相当于在dijkstra 搜索的过程中，每探测到一个node,都需要判断是不是在Cell C的范围内。因此，在搜索之前我们把Cell C 在overlay graph 中相应部分复制一份，在复制的这份中进行搜索。

对搜索图进行剪枝

在对搜索图搜索之前，合并图中所有出度为1的内部节点合并，可以缩减图的搜索范围。这个方法是基于boundary arc大多数都是出度为1的边这一事实。

使用其他搜索算法

使用Bellman-Ford算法进行最短路径搜索，此算法在较小的graph中的搜索性能相比Dijkstra优秀，crp中分割的每个cell属于较小的graph,适应于Bellman-Ford算法。

Multiple-source executions

将多个source的Dijkstra算法合并成一个执行过程可以优化算法执行时间。

并行计算

multipe-source execution的特征符合SIMD(single instruction,multiple data)指令，利用SSE寄存器可以实现指令级别的并行运算；除此之外，我们可以把每个cell的搜索分配到不同的核上进行并行计算。

Phantom Levels

因为customization的过程在处理较小的图的时候性能较好，因此使用更多的level 可以加速customization。过多level的坏处是带来更高的空间复杂度，因此我们引入一个phantom level,此level只是在customization的时候使用，在query的时候不使用。

使用定制化的ch算法加速

ch 在进行contraction 之前需要确定contraction order,找到一个完美的contraction order是一个NP-hard问题，crp算法为了使contraction order 做到对所有的metric都适用，采用基于edge-difference计算contraction order。由于这个contraction order和metric相互独立，所以contracion order 在partition部分计算。
除此之外，为了加速contraction,crp在工程实现时候利用microinstructions加速计算。

增量更新

在更新实时路况时，crp算法可以做到只更新对应level 的overlay graph。其他没被影响的cell的customization不用计算。

---

Query

首先介绍query level 的概念：对于任何一个node v ,query level 代表和{s,t}没有交集的最大level。为了加速查找query level,crp 针对每一个node,将表示node所在的level以及对应的cell num编码到一个64位整形中。
query level 这个概念的含义如下，对于multipel-level overlay graph 来说，越高level的图越稀疏，搜索效率越高，但是当level高到同时包括s,t,v三个node时，图的粒度太大，无法找到最优路径。换句话说，crp 算法加速搜索的原理是，当搜索到不包含s或者t的cell的时候，我们不需要搜索其cell内部的路径只需要使用customization 过程中计算的shortcut 代替即可。

Unpack Path

同ch 算法不同，crp 为了节省内存，没有存储shortcut 对应的原始路径，而是在还原道路时候对于每个shortcut 使用双向dijkstra 算法计算出最短路径。这种做法会牺牲一些响应时间，crp 算法利用一个lru cache在内存占用和响应时间之间取折中。